Universal Functions
There are two types of Array state: middle state and ending state.
Ending state have assignment notation, but middle state don't have assignment.
For example:
Ending state: B = np.arange(3)
Middle state: np.exp(B)
NumPy provides mathematical functions such as sin, cos, and exp.
These functions are called “universal functions”(ufunc).
These functions operate elementwise on an array, producing an array as output.
The following example codes illustrate the function of “arrange”, “exp”, “sqrt”, “add”.
























Indexing, Slicing and Iterating
In numpy, array slicing is compose by start, stop, step.
array slicing is similar to python list slicing
There are three format of array indexing and slicing
1 array [ num1 ]=> index the single element in location "num1"
2 array [ num_start: num_end ]
=> slice the elements between location "num_start" and "num_end", but not including offset num_end
3 array [ num_start:num_end: step_size ] => slice for the elements between location "num_start" and "num_end", step "step_size"
The following example codes illustrate the function of “arrange”, “**”and array slicing.
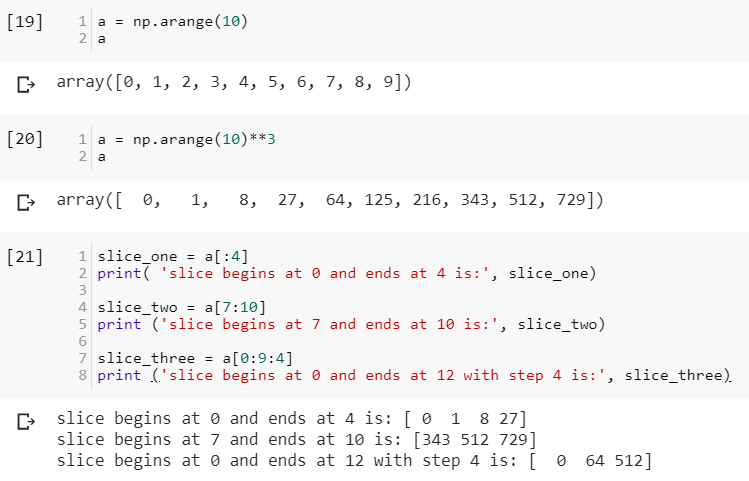
The following example codes illustrate more about array slicing function.

Multidimensional arrays can have one index per axis. Take some examples by 2D array
- [ num1,num2] : single element in 2D array
- [, num1]: a column of elements in num1
[num1, ]: a raw of elements in num1
[num1: num2]: from raw num1 to raw num2. Skip num1 means 0





When fewer indices are provided than the number of axes, the missing indices are considered complete slices:

The expression within brackets in b[i] is treated as an i followed by as many instances of : as needed to represent the remaining axes. NumPy also allows you to write this using dots as b[i,...].
The dots (...) represent as many colons as needed to produce a complete indexing tuple. For example, if x is an array with 5 axes, then
x[1,2,...] is equivalent to x[1,2,:,:,:], x[...,3] to x[:,:,:,:,3] and x[4,...,5,:] to x[4,:,:,5,:].

Iterating over multidimensional arrays is done with respect to the first axis:

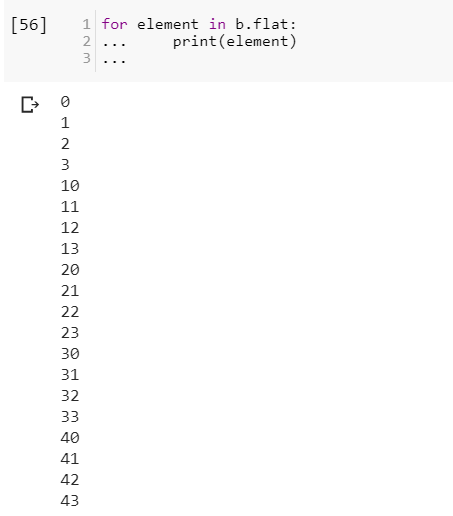
However, if one wants to perform an operation on each element in the array, one can use the flat attribute which is an iterator over all the elements of the array:
Changing the shape of an array
In this section, several NnmPy functions will be illustrated, including:
- shape()
- reveal()
- reshape()
- T()
- resize()
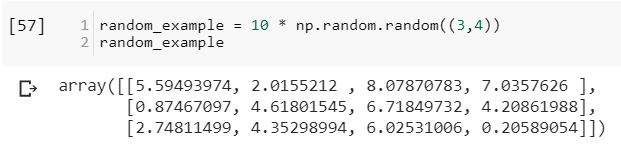
Moreover, only the function resize() would change the old array content. The following example generate an example array by random() function.
An array has a shape given by the number of elements along each axis:

The shape of an array can be changed with various commands. Note that the following three commands all return a modified array, but do not change the original array
The order of the elements in the array resulting from ravel() is normally “C-style”, that is, the rightmost index “changes the fastest”, so the element after a[0,0] is a[0,1]. If the array is reshaped to some other shape, again the array is treated as “C-style”. NumPy normally creates arrays stored in this order, so ravel() will usually not need to copy its argument, but if the array was made by taking slices of another array or created with unusual options, it may need to be copied. The functions ravel() and reshape() can also be instructed, using an optional argument, to use FORTRAN-style arrays, in which the leftmost index changes the fastest.

The reshape function returns its argument with a modified shape, whereas the ndarray.resize method modifies the array itself:


If a dimension is given as -1 in a reshaping operation, the other dimensions are automatically calculated:
