Word Embedding
2018/3/20 Tsung-Yu Tsai
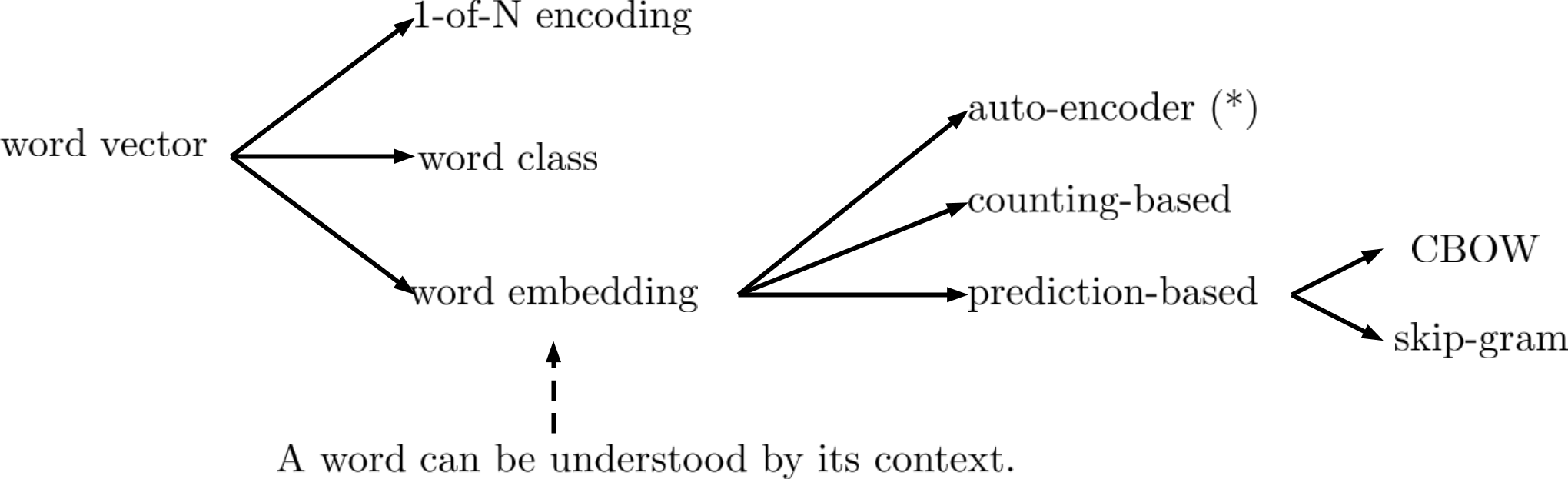
圖0 Schematic of Word Embedding Document
Word Embedding 是一個廣為人知Unsupervised Learning: Dimension Reduction的應用。
如果要用一個Vector表現一個word,最typical的作法是1-of-N encoding ,N就表示所有Word的數目,每個word對應到其中的一維。例如:如果我們要辨識10萬個Word的話,N就等於10萬。1-of-N encoding的缺點是很難得到word彼此之間的關係,所以Vector一點都不informative,例如:cat vs dog其實都是動物,但是在1-of-N encoding卻是兩個獨立向量。
另外一種用Vector表示word的方法是word class,就是預先把所有的word分成幾大類(class),用這些類(class)的index來表示,這個就等同於Dimension reduction裡面的clustering。不過word class還是無法很好表示word跟word之間的關係。
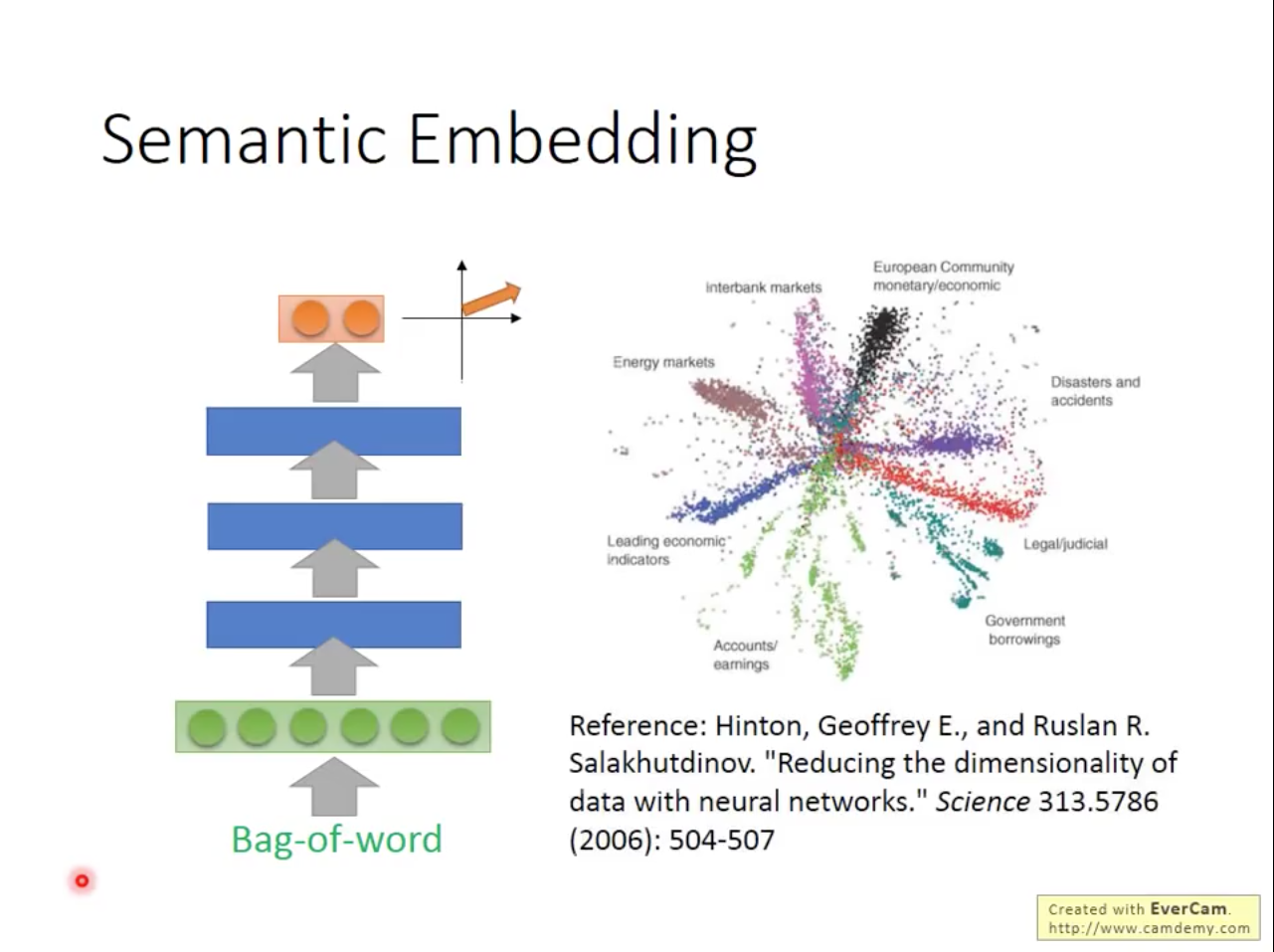
Word Embedding是把word投影到一個高維的空間(雖然是高維,但是維度仍然遠小於所有詞的數量),這個投影(project)能夠滿足:
- similar words are closer
- each dimension has unique semantic meaning
為什麼word embedding是unsupervised learning?因為我們有明確的input,但是沒有明確的output。那我們能不能用Auto-encoder來做word embedding呢?從前人的研究結果顯示,Auto-encoder並不是一個好的model,如果我們是用1-of-N encoding當作input的話,auto-encoder完全沒辦法學到有用的訊息。如果是用character-level encoding例如:N-gram,可能可以抓到一個字首字根的關係,但是還沒有word之間的關係。
Word Embedding 的基礎是:A word can be understood by its context,例如:馬英九520宣誓就職 vs 蔡英文520宣誓就職,雖然機器不曉得蔡英文跟馬英文是什麼意思,但是從給出的句子,機器可以學到馬英九跟蔡英文應該是相似的詞。裡面又可以更細分為counting-based跟prediction-based
Counting-based vs Prediction-based Word Embedding
Counting-based method 是計算兩個詞在context裡面同時出現的機率來計算兩個詞的相似度。以Glove Vector為例,對於兩個word ,對word embedding function , 跟兩個詞在文章中同時出現的次數 要盡量靠近。
Prediction based approach 如圖一所示,給一個 word ,它能夠預測下一個word 是誰?整個神經網路把的1-of-N encoding當作input,經過網路的計算,output代表每個word是 的機率。經過充分訓練之後,我們取該網路第一層neurons的值當作我們的word vector ,用它來代表word 。
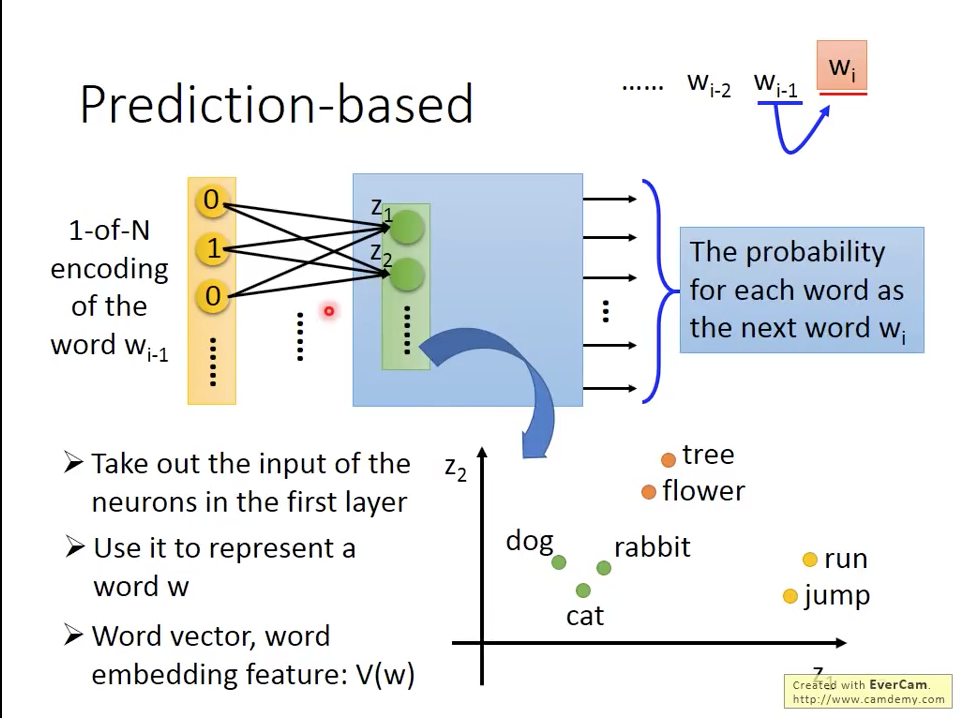
圖一 Prediction-based Word Embedding
同樣的原理,我們也可以使用N個word 來預測下一個word ,我們用一個N=2的model,如圖二所示:
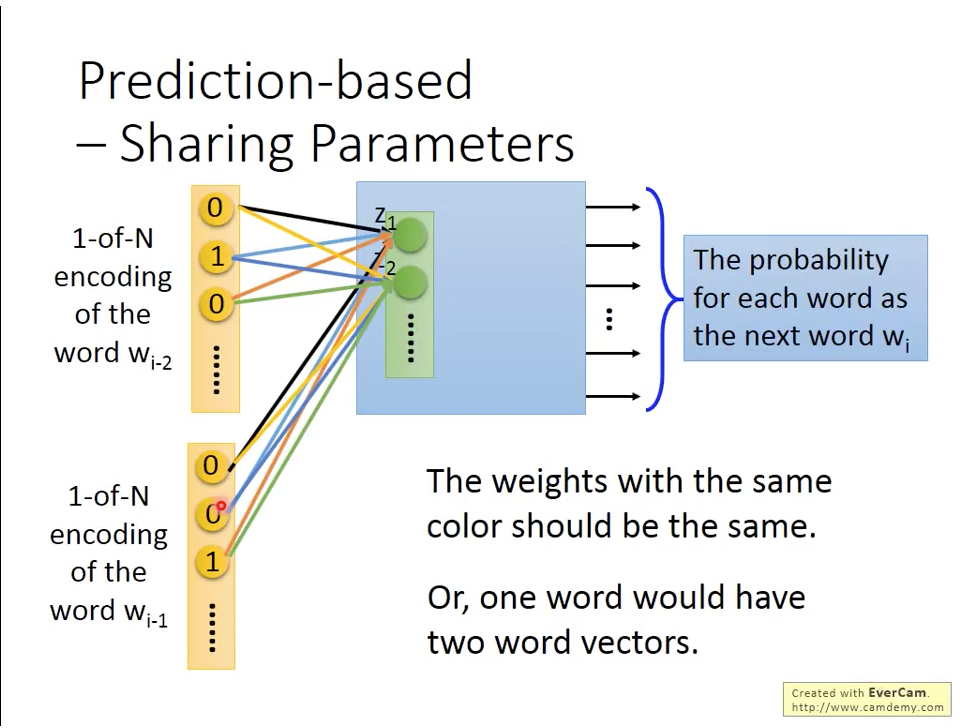
圖二 N-word Prediction-based Word Embedding
跟 的1-of-N encoding 和 的維度都是 ,word embedding vector 維度是 。根據圖二, 是 , 的線性組合。
通常我們會讓,代表我們對於各個word的權重是共享的。原因有兩個,一個原因顯而易見,就是降低要訓練的權重數量,第二個的原因是如果每個時間點的權重不一樣的話,代表我們是相同的word在不同時間點會產生不同的word vector。那我們在訓練的時候如何保持權重相同,方式就是在原本back-propagation更新時,除了自己的偏微分之外,也加入其他同層參數的偏微分,如下面的公式:
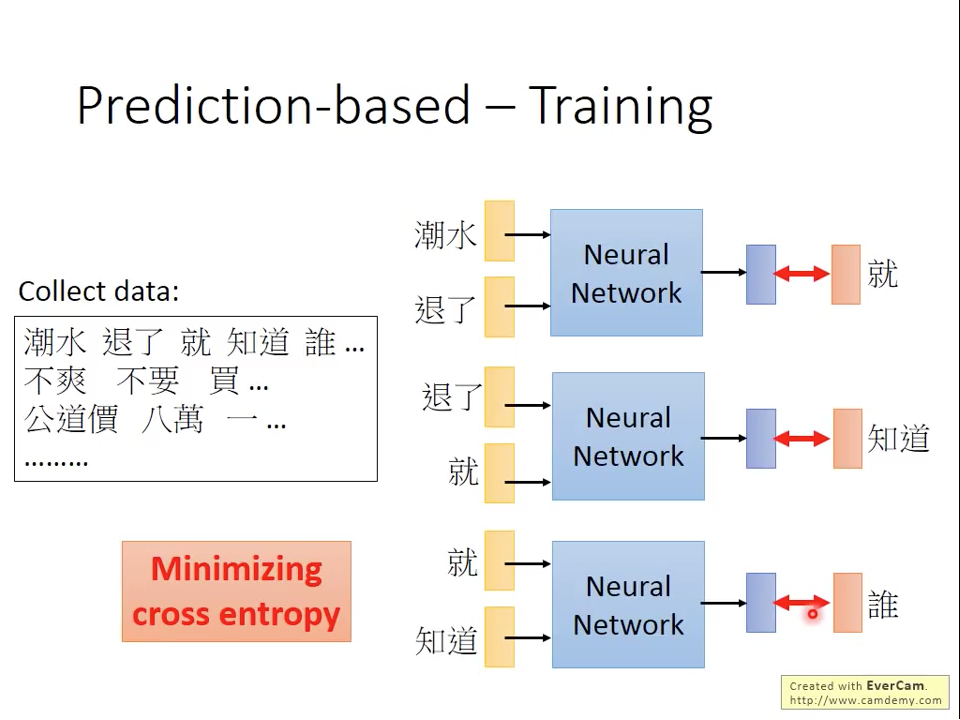
圖三 Prediction-based Training
在Word Embedding的架構裡面,最常使用的架構有兩種:
- Continous Bag-of-Word (CBOW) model
- skip-gram model
兩個各有擅長,不分上下。主要的差異如圖四所示,CBOW是使用前後的word當輸入來預測現在出現的詞彙;skip-gram是用現在的詞彙當輸入,來預測前後會出現的詞彙。
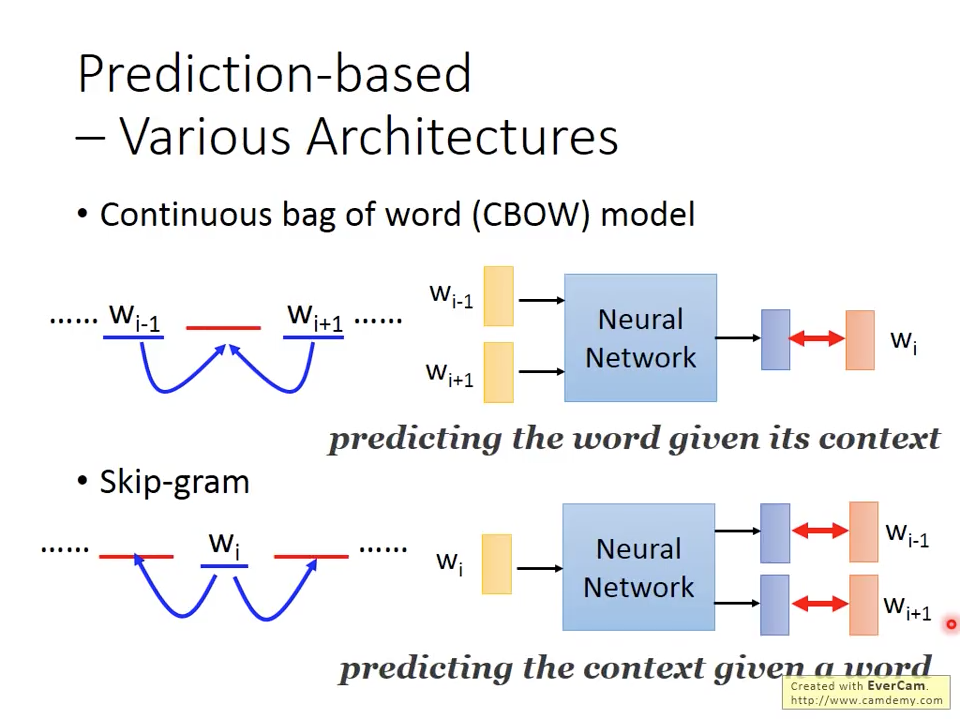
圖四 CBOW model vs skip-gram model
Characteristic and Application of Word Embedding

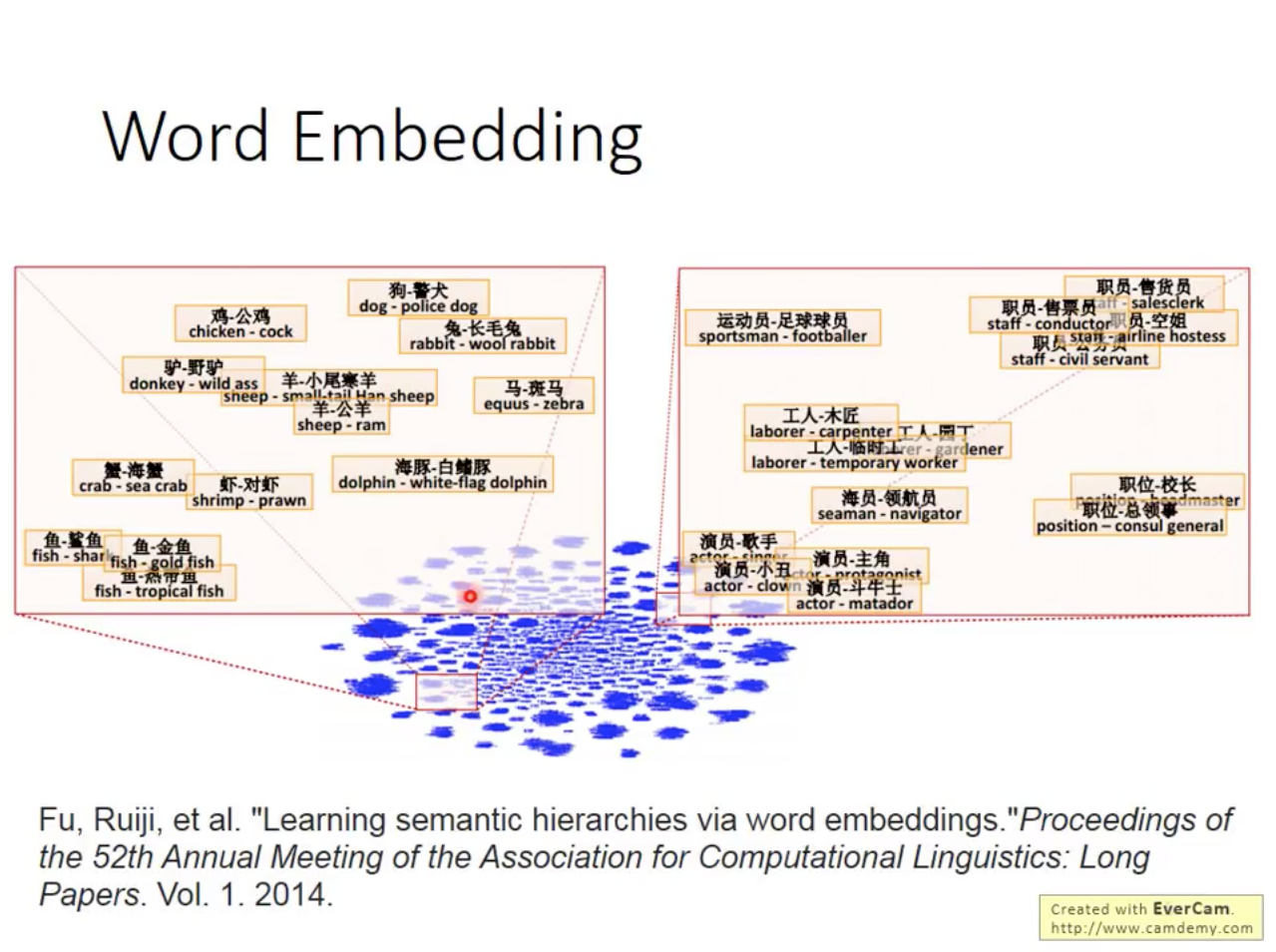

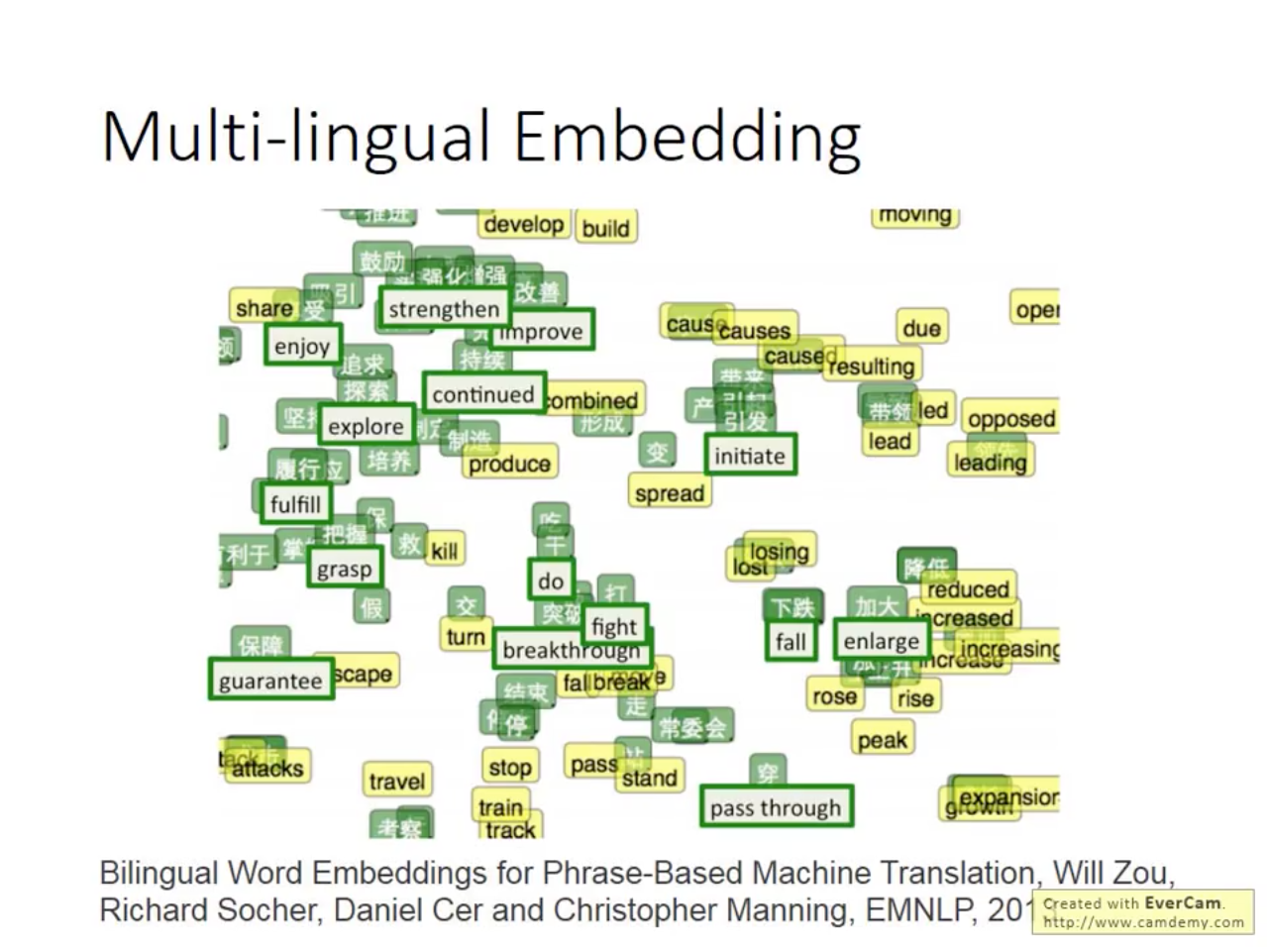
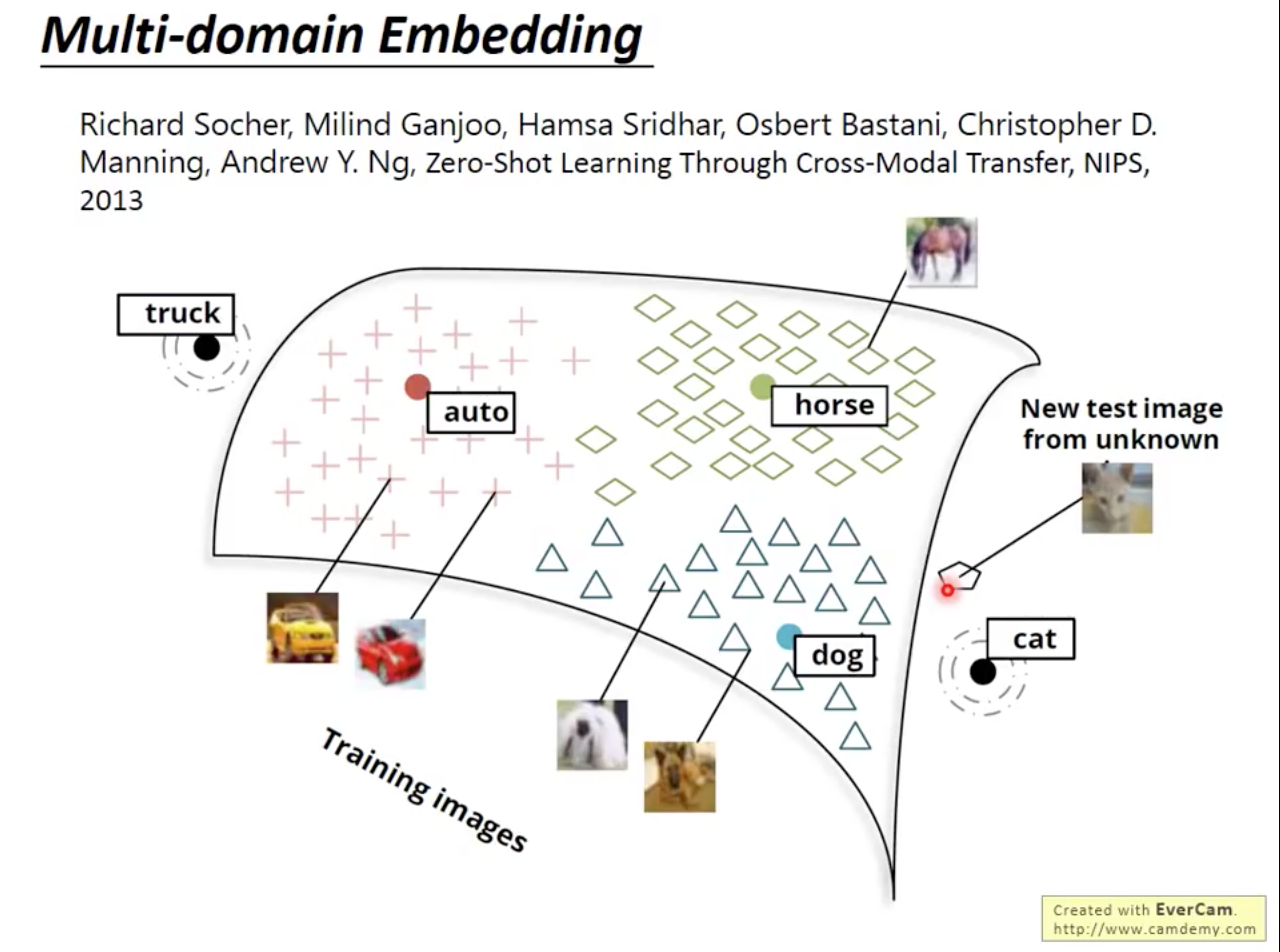



[0]
H. Y. Lee, ML lecture #14, Word Embedding, at https://www.youtube.com/watch?v=X7PH3NuYW0Q&t=1846s