CBOW Model with One-word Context
The CBOW model predicts one word by its context words (input of CBOW model) [1].
Define a vocabulary containing V words as
V={d1,d2,⋯,dk,⋯,dV}
where dk is the k-th word in the vocabulary. The training corpus C can be constituted by Na articles as C={article1,article2,⋯, articleNa}.

Fig.1. Schematic of a word sequence and an article.
Fig.1. shows the schematic of a word sequence and an article. A word sequence is formed by concatenating the words in the vocabulary V. Each article is formed by concatenating n word sequences.
Considering the context word being one word, the CBOW is reduced to a bigram model.
 Fig.2. Data flow of CBOW model with one-word context.x¯k is the one-hot encoded vector of word dk and is input to the NN for CBOW model with one-word context. y¯ is the output of the NN. The input word vector representation w¯k and output word vector representation w¯j′ are two kinds of word vector representations.
Fig.2. Data flow of CBOW model with one-word context.x¯k is the one-hot encoded vector of word dk and is input to the NN for CBOW model with one-word context. y¯ is the output of the NN. The input word vector representation w¯k and output word vector representation w¯j′ are two kinds of word vector representations.
Fig.2. shows the data flow of CBOW model with one-word context.The word dk is one-hot encoded into x¯k and x¯k is input to the neural network (NN) for CBOW model with one-word context, expanded as
x¯k=[x1k,x2k,⋯,xk−1k,xkk,xk+1k,⋯,xVk]t(1)
where xnk=0 for n≠k and xkk=1; t stands for transpose operation.
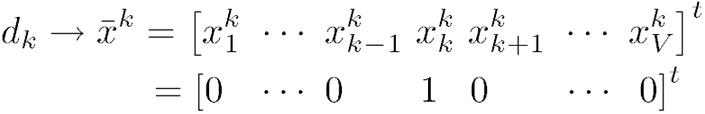
Fig.3 Schematic of one-hot encoding for k-th word, dk→x¯k=[x1k,x2k,⋯,xkk,⋯,xVk]t=[0,⋯,1,⋯,0]t
Fig.3 shows the schematic of one-hot-encoding for k-th word dk.
The output y¯=[y1,⋯,yj,⋯,yV]t has the size of V; yj=p(dj∣x¯k) is a probability that the next word is dj given the one-hot encoded vector x¯k with the property that j=1∑Vyj=1.
The NN is trained by inputting the articles in the training corpus C to the NN word by word with the given context word dk and its corresponding target word djt. jt is the index of the target word.

Fig.4 Schematic of the target word djt under CBOW model of one-word context dk. (a) dk=d17, djt=d17. (b) dk=d21, djt=d77.
Fig.4 shows the schematic of the target word under CBOW model of one-word context. The target word is the next word of the given context word in the word sequence.
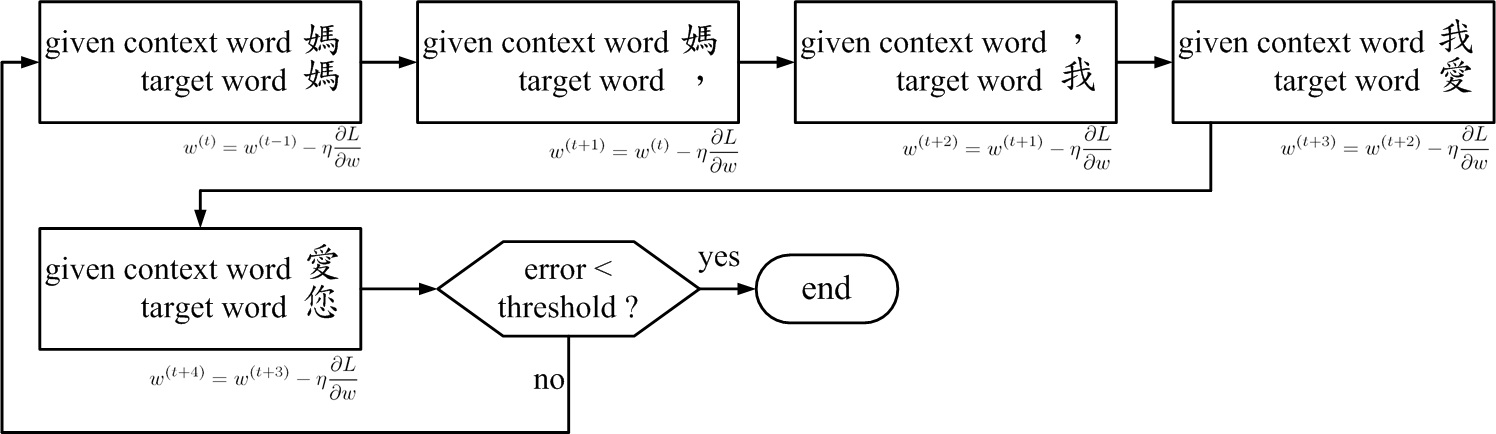 Fig.5. Overall training flow-chart of the example "媽媽,我愛您".
Fig.5. Overall training flow-chart of the example "媽媽,我愛您".
Fig.5 shows the overall training flow-chart of the example "媽媽,我愛您".
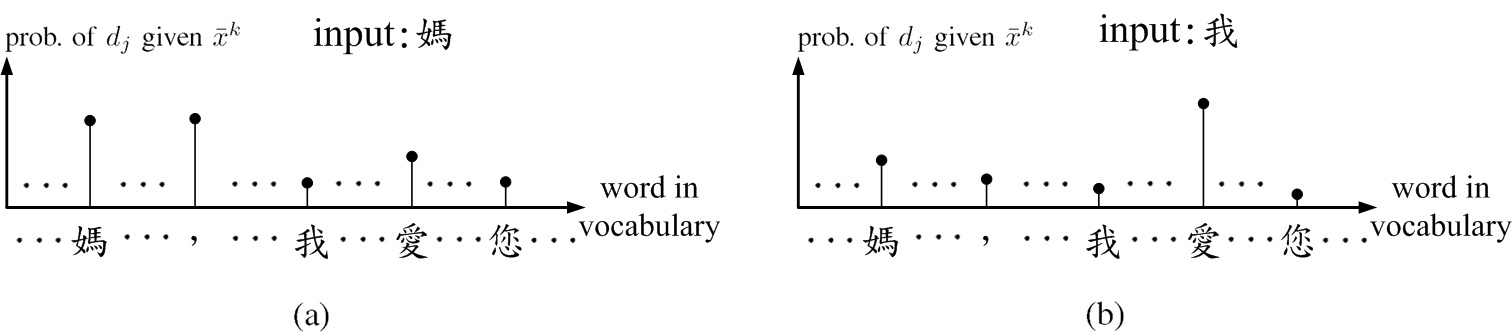 Fig.6. Schematic of output y¯ of a well-trained NN given x¯k in a testing example. (a) input "媽", (b) input "我".
Fig.6. Schematic of output y¯ of a well-trained NN given x¯k in a testing example. (a) input "媽", (b) input "我".
Fig.6 shows the schematic of output y¯ of a well-trained NN given x¯k in a testing example for input words "媽" and "我". As testing a well-trained NN with input word "媽", one finds that the probabilities of "媽" and "," might be higher than most other words in the vocabulary. As inputting "我", the probability of "愛" might be higher than most other words in the vocabulary.
The input word vector representation w¯k and output word vector representation w¯j′ are two kinds of word vector representations.
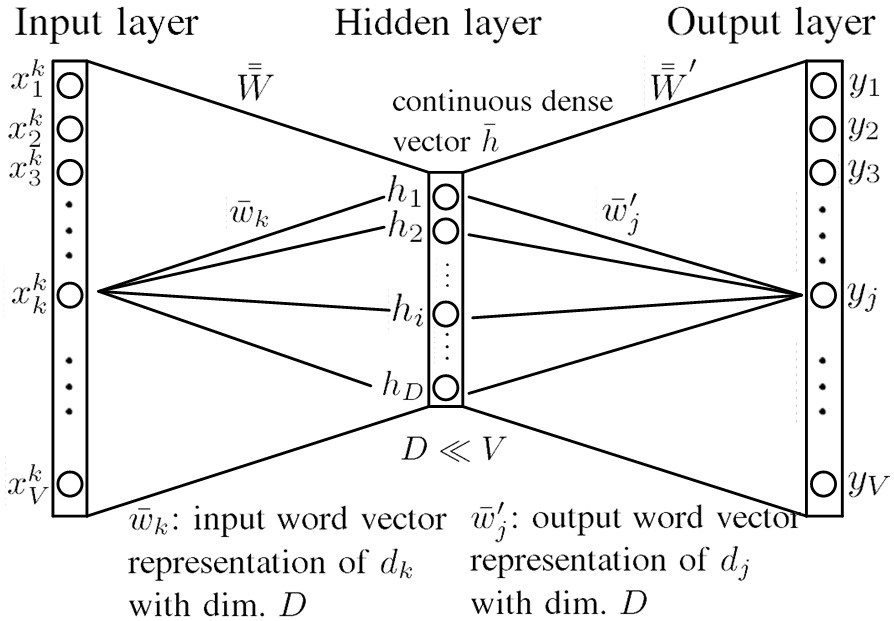
Fig.7. Architecture of the NN for the CBOW model with one context word. w¯k is input word vector representation of dk, and w¯j′ is output word vector representation of dj. Both of w¯k and w¯j′ are of dimension D, D≪V.
Fig.7 shows the architecture of the NN for the CBOW model with one context word.W¯¯ and W¯¯′ are the input-to-hidden and hidden-to-output weight matrices. w¯k is input word vector representation of dk and w¯j′ is output word vector representation of dj. The neuron numbers in the input layer and in the output layer are both chosen to be the vocabulary size V, and the hidden layer size is D. Usually, D≪V. For example, V=8000 and D=60 or 100.
Forward Propagation
The input-to-hidden weight between the neuron k in the input layer and the neuron i in the hidden layer is denoted as wki , forming a V×D weight matrix as
W¯¯=⎣⎢⎢⎢⎢⎢⎢⎡w11w21⋮wk1⋮wV1w12w22⋯⋯⋯wV2⋯⋯⋱wki⋱⋯⋯⋯⋯⋯⋯⋯w1Dw2D⋮wkD⋮wVD⎦⎥⎥⎥⎥⎥⎥⎤(2)
where the k-th row of W¯¯ contains the weights whcih connect the neuron k in the input layer to all neurons in the hidden layer as shown in Fig.6. Define the transpose of the k-th row of W¯¯ as the input word vector representation w¯k, namely,
w¯k≐[wk1,⋯,wki,⋯,wkD]t
which is the D-dimensional vector representation of the input word dk.
The hidden-layer output is obtained as
h¯=W¯¯tx¯k
=⎣⎢⎢⎢⎢⎡w11w12⋮⋮w1Dw21w22⋯⋯w2D⋯⋯⋯⋱⋯wk1⋯wki⋯wkD⋯⋯⋯⋮⋯wV1wV2⋮⋮wVD⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡0⋮0xkk=10⋮0⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡wk1⋮wki⋮wkD⎦⎥⎥⎥⎥⎤=w¯k(3)
The hidden-to-output weights are denoted as wij′, which connect the neuron i in the hidden layer and the neuron j in the output layer and form an D×V weight matrix W¯¯′ as
W¯¯′=⎣⎢⎢⎢⎢⎢⎢⎡w11′w21′⋮wi1′⋮wD1′w12′w22′⋯⋯⋯wD2′⋯⋯⋱⋯⋱⋯w1j′w2j′⋯wij′⋯wDj′⋯⋯⋯⋯⋯⋯w1V′w2V′⋮wiV′⋮wDV′⎦⎥⎥⎥⎥⎥⎥⎤(4)
where the j-th column contains the weights which connect all neurons in the hidden layer to the j-th neuron in the output layer as shown in Fig.2. Define the j-th column of W¯¯′ as the output vector v¯j′, namely,
w¯j′≐[w1j′,w2j′,⋯,wij′,⋯,wDj′]t(5)
Note that the output vector w¯k′ is another D-dimensional vector representation of the input word dk. By substituting (5) into (4), we can represent W¯¯′ as
W¯¯′=[w¯1′,⋯,w¯j′,⋯,w¯V′](6)
The vector h¯ in (3) is weighted by W¯¯′ to obtain the input of the output layer as
u¯=W¯¯′t⋅h¯=⎣⎢⎢⎢⎢⎡w11′w12′⋮⋮w1V′w21′w22′⋮⋮w2V′⋯⋯⋱⋮⋯wi1′⋮wij′⋮wiV′⋯⋯⋯⋱⋯wD1′wD2′⋮⋮wDV′⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡wk1⋮wki⋮wkD⎦⎥⎥⎥⎥⎤=[w¯1′,⋯,w¯j′,⋯,w¯V′]tw¯k
which can be represented as
u¯=[w¯1′,⋯,w¯j′,⋯,w¯V′]tw¯k=⎣⎢⎢⎢⎢⎡u1⋮uj⋮uV⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡w¯1′tw¯k⋮w¯j′tw¯k⋮w¯V′tw¯k⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡w¯1′⋅w¯k⋮w¯j′⋅w¯k⋮w¯V′⋅w¯k⎦⎥⎥⎥⎥⎤(7)
The output yj of the j-th neuron in the output layer is a probability that the next word is dj given the one-hot encoded vector x¯k as
yj=p(dj∣x¯k)=j=1∑Veujeuj=j=1∑Vew¯j′⋅w¯kew¯j′⋅w¯k(8)
The training objective is to maximize the probability yjt of observing the target word djt given x¯k.
The loss function is defined as
L=−lnp(djt∣x¯k)(9)
Note that maximizing yjt=p(djt∣x¯k) is to minimize L.
Backward Propagation
By using (8), the loss function is expressed as
L=−lnyjt=−ujt+ln(j=1∑Veuj)(10)
The partial derivative of L with respect to uj is
∂uj∂L=yj−y^j(11)
where we define the desired output y^j as
y^j={0,1,j≠jtj=jt
The supporting material of (11) is
∂ujt∂L=−1+j=1∑Veujeujt=yjt−1∂uj∂L=∂yjt∂L∂uj∂yjt=−yjt1∂uj∂yjt=−yjt1∂uj∂∑j=1Veujeujt=−yjt1eujt∂uj∂(j=1∑Veuj)−1=−yjt1eujt[−(j=1∑Veuj)−2]∂uj∂(∑j=1Veuj)=yjt1∑j=1Veujeujt∑j=1Veujeuj=yjtyjtyj=yj, j≠jt
Thus, we can define the error between the NN output and the desired output as
e¯=y¯−y^ or ej=yj−y^j(12)
where y^=[y^1,⋯,y^j,⋯,y^V]t.
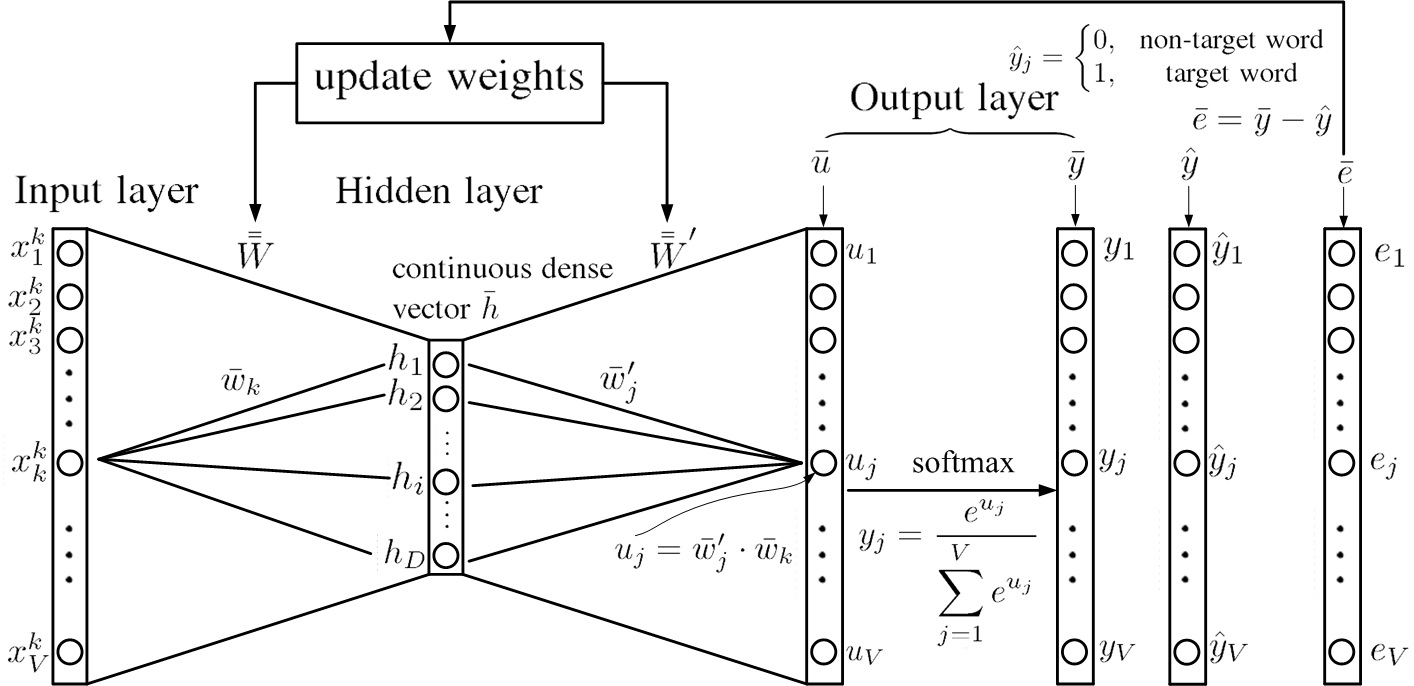 Fig.8. Overview of updating weights of the NN for CBOW model.
Fig.8. Overview of updating weights of the NN for CBOW model.
Fig.8 shows the overview of updating weights of the NN for CBOW model.
The derivative of L to the hidden-to-output weight wij′ is
∂wij′∂L=∂uj∂L∂wij′∂uj=ejwki(13)
The supporting material of (13) is
uj=w¯j′⋅w¯k∂wij′∂uj=i=1∑Nwij′wki=wki
By using stochastic gradient descent, we obtain the updating equation for hidden-to-output weights wij′ as
wij′(new)=wij′(old)−η∂wij′∂L=wij′(old)−ηejwki(old)(14)
or equivalently
w¯j′(new)=w¯j′(old)−ηejw¯k(old)(15)
where η>0 is the learning rate.
Since at j≠jt, ej>0, which is called overestimating and can be seen in (12), that w¯j′(old) subtract a scaled w¯k(old) in (15) leads to the angle between w¯j′(new) and w¯k(old) increasing. Since at j=jt, ej<0, which is called underestimating, that w¯j′(old) add a scaled w¯k(old) in (15) leads to the angle between w¯j′(new) and w¯k(old) decreasing. If yjt is close to 1, the error is close to 0 and w¯jt′ is nearly unchanged.
Next, find the update equation for input-to-hidden weights W¯¯. The derivative of L to the output of the hidden layer hi is
∂hi∂L=j=1∑V∂uj∂L∂hi∂uj=j=1∑Vejwij′(16)
The supporting material of (16) is
hi=wki
and
∂hi∂uj=∂wki∂uj=wij′
The derivative of L to the input-to-hidden weights wki is
∂wki∂L=∂hi∂L∂wki∂hi=∂hi∂L=j=1∑Vejwij′(17)
The update equation for input-to-hidden weights wki is
wki(new)=wki(old)−η∂wki∂L=wki(old)−ηj=1∑Vejwij′(old)(18)
or
w¯k(new)=w¯k(old)−ηj=1∑Vejw¯j′(old)(19)
The input word vector representation w¯k is updated by adding the sum of scaled output word vector representations w¯j′. At j≠jt (ej>0) , the contribution of w¯j′ will put w¯k farther away from w¯j′. At j=jt (ej<0), the contribution of w¯jt′ will move w¯k closer to w¯jt′. If the contribution of all the output word vectors is nearly zero, the input word vector remains nearly unchanged.
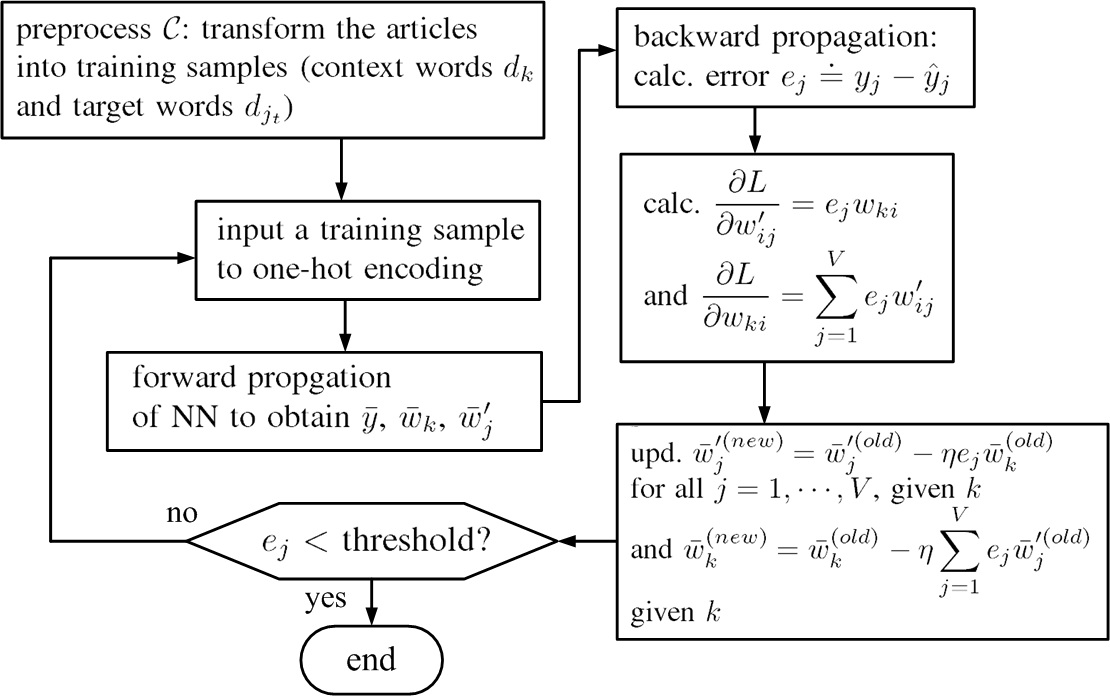 Fig.9. Flow-chart to train distributed vector representations of words in vocabulary V by a training corpus C.
Fig.9. Flow-chart to train distributed vector representations of words in vocabulary V by a training corpus C.
Fig.9. shows a flow-chart to train distributed vector representations of words in vocabulary V by a training corpus C.
[0]
X. Rong, word2vec parameter learning explained, arXiv:1411.2738, 2014.
[1]
T. Mikolov, K. Chen, G. Corrado and J. Dean, Efficient estimation of word representations in vector space,
arXiv:1301.3781, 2013.

 Fig.2. Data flow of CBOW model with one-word context. is the one-hot encoded vector of word and is input to the NN for CBOW model with one-word context. is the output of the NN. The input word vector representation and output word vector representation are two kinds of word vector representations.
Fig.2. Data flow of CBOW model with one-word context. is the one-hot encoded vector of word and is input to the NN for CBOW model with one-word context. is the output of the NN. The input word vector representation and output word vector representation are two kinds of word vector representations.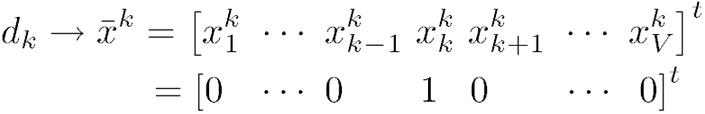

 Fig.5. Overall training flow-chart of the example "媽媽,我愛您".
Fig.5. Overall training flow-chart of the example "媽媽,我愛您". Fig.6. Schematic of output of a well-trained NN given in a testing example. (a) input "媽", (b) input "我".
Fig.6. Schematic of output of a well-trained NN given in a testing example. (a) input "媽", (b) input "我".
 Fig.8. Overview of updating weights of the NN for CBOW model.
Fig.8. Overview of updating weights of the NN for CBOW model. Fig.9. Flow-chart to train distributed vector representations of words in vocabulary by a training corpus .
Fig.9. Flow-chart to train distributed vector representations of words in vocabulary by a training corpus .