CBOW Model with Multi-word Context

The CBOW model predicts one target word by its context words [1].

Consider a vocabulary containing V words can be expressed as

${\mathcal V} = \{ d_1, d_2, \cdots, d_k, \cdots, d_V\}$

where $d_k$ is the $k$-th word in the vocabulary. The training corpus ${\mathcal C}$ can be constituted by $N_a$ articles as

${\mathcal C} = \{ {\textrm article}_1, {\textrm article}_2, \cdots, {\textrm article}_{N_a} \}$

.Each article is constituted by the words in the vocabulary ${\mathcal V}$. For example,

${\textrm article}_1 = 'd_1 \ d_5 \ d_{18} \ d_{56} \ d_2 \ \cdots '$

The $C$-word context of target word $d_{j_o}$ in an article is defined as

$C_x (d_{j_o}) = \left\{ d_{c_m}| d_{c_m} \textrm{ is the word in the context of } d_{j_o}, m = 1, 2, \cdots, C \right\} \pod{\text{1}}$

where the subscript $c_m$ can be the integers between $1$ and $V$. For example, in ${\textrm article}_1$, the first 4-word context of $d_{18}$ is

$C_x (d_{18}) = \{ d_{c_1}, d_{c_2}, d_{c_3}, d_{c_4} \} = \{ d_1, d_5, d_56, d_2 \}$

Fig.1. Data flow of CBOW model with $C$-word context.$\bar{x}^{c_1}, \cdots, \bar{x}^{c_C}$ are the one-hot encoded vectors of words $d_{c_1}, \cdots, d_{c_C}$ and are input to the NN at the same time for CBOW model with $C$-word context. $\bar{y}$ is the output of the NN. The input vectors $\bar{v}_{c_1}, \cdots, \bar{v}_{c_C}$ and output vector $\bar{v}_j'$ are two kinds of word vector representations.

Fig.1. shows the data flow of CBOW model with $C$-word context.The words in the context $C_x(d_{j_o})$ are all one-hot encoded into $\bar{x}^{c_1}, \cdots, \bar{x}^{c_C}$ which are input to the neural network (NN) for the CBOW model.The output $\bar{y} = [y_1, \cdots, y_j, \cdots, y_V]^t$ has the size of $V$ and $y_j$ is a probability that the target word is $d_j$ given the one-hot encoded vectors $\bar{x}^{c_m}$, $m = 1,\cdots, C$. The input vectors $\bar{v}_{c_m}, m = 1, \cdots, C$ and output vector $\bar{v}_j'$ are two kinds of word vector representations and will be elaborated later.The NN is trained by inputting the articles in the training corpus ${\mathcal C}$ to the NN word by word.

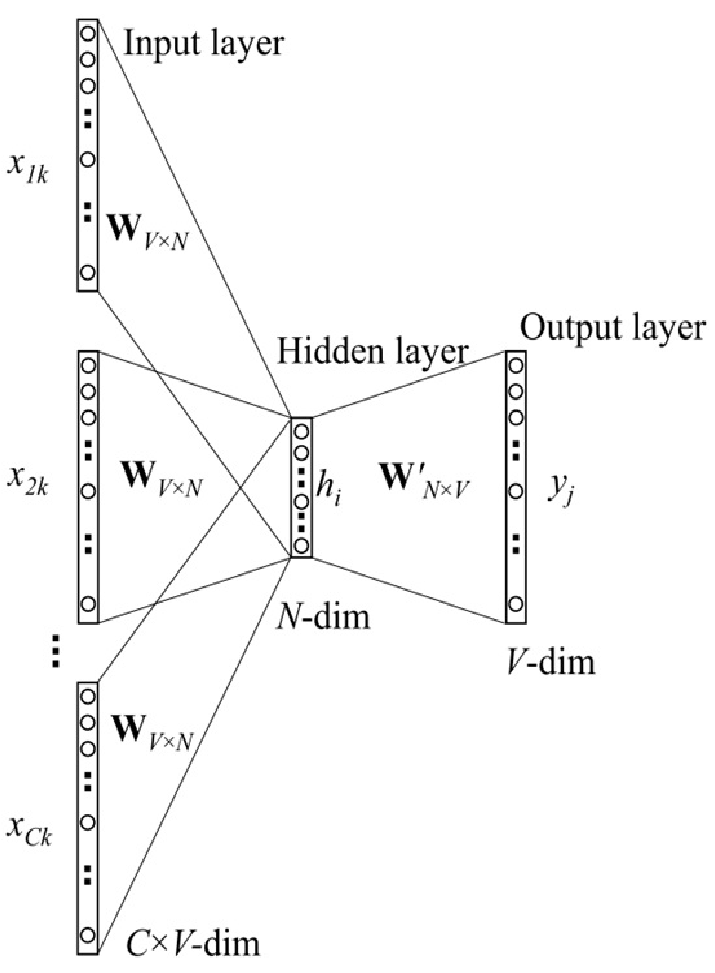
Fig.1. Architecture of the NN for CBOW model with $C$ context words of the target word $d_{j_o}$.

Fig.1. shows the architecture of the NN for CBOW model with $C$ context words of the target word $d_{j_o}$. A softmax function is still imposed at the end of the output layer.

The hidden layer output is calcuted as

$\bar{h} = \frac{1}{C} \bar{\bar{W}}^t \cdot \left( \bar{x}_{c_1} + \bar{x}_{c_2} + \cdots + \bar{x}_{c_C} \right) = \frac{1}{C} \left( \bar{v}_{w_{c_1}} + \bar{v}_{w_{c_2}} + \cdots + \bar{v}_{w_{c_C}} \right) \pod{\text{2}}$

or represented component-wise as

$h_i = \frac{1}{C} \sum_{m = 1}^C w_{c_m i}, \ i = 1, 2, \cdots, N \pod{\text{3}}$

The output of the neural network at $j$-th neuron is the probability of word $w_j$ given the context of $w_{j_o}$, namely,

$y_j = p(w_j | Cx(w_{j_o}) ) = \frac{e^{\bar{v}_{w_j}' \cdot \bar{h}} }{\displaystyle \sum_{j = 1}^V e^{\bar{v}_{w_j}' \cdot \bar{h}}} \pod{\text{4}}$

The loss function is defined as

$E = -\ln p(w_{j_o}| Cx(w_{j_o})) \pod{\text{5}}$

[0]

X. Rong, word2vec parameter learning explained, arXiv:1411.2738, 2014.

[1]

T. Mikolov, K. Chen, G. Corrado and J. Dean, Efficient estimation of word representations in vector space,

arXiv:1301.3781, 2013.