Attention-based Multi-hop Recurrent Neural Network (AMRNN) Model

MM 05/24/2018

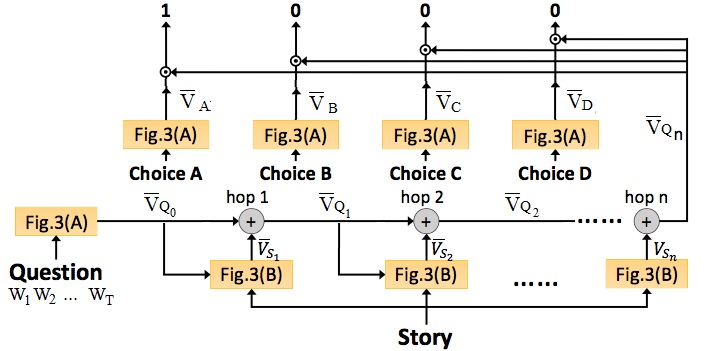
Fig. 2 The overall structure of the proposed Attention-based Multi-hop Recurrent Neural Network (AMRNN) model.

Fig.2 shows the overall structure of the AMRNN model.

The input of model includes the transcriptions of an audio story, a question and four answer choices, all represented as word sequences. The word sequence of the input question is represented as a question vector $\bar{V}_{Q_0}$.

The attention mechanism is applied to extract the question-related information from the story.

The machine then goes through the story by the attention mechanism several times (from $\bar{V}_{Q_0}$ ,$\bar{V}_{Q_1}$,$\bar{V}_{Q_2}$ ,$\cdots$), and obtain an answer selection vector $\bar{V}_{Q_n}$. This answer selection vector is used to evaluate the confidence of each choice ($\bar{V}_A$, $\bar{V}_B$, $\bar{V}_C$ and $\bar{V}_D$), and the choice with the highest score is taken as the output.

All the model parameters are jointly trained with the target where 1 for the correct choice and 0 otherwise.

Question Representation

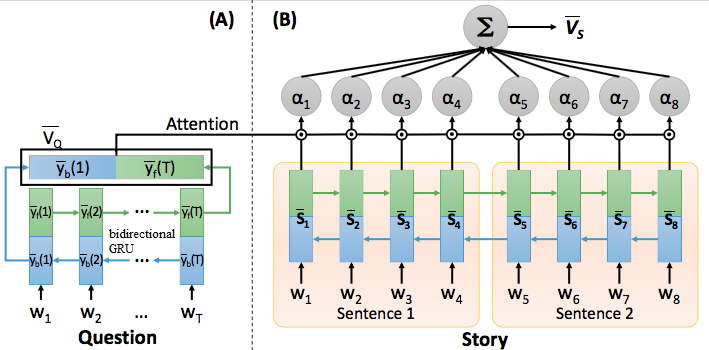
Fig. 3 (A) The Question Vector Representation and (B) The Attention Mechanism.

Fig.3 (A) shows the procedure of encoding the input question into a vector representation $\bar{V}_Q$.

The input question is a sequence of $T$ words, $w_1,w_2, \cdots, w_T$, every word $w_t$ represented in 1-of-N encoding.

A bidirectional Gated Recurrent Unit (GRU) network [1]-[3] takes one word from the input question sequentially at a time.

In other words, $w_t$ is the input word at time $t$.

In Fig.3(A), the hidden layer output of the forward GRU (green rectangle) at time index $t$ is denoted by $\bar{y}_f(t)$, and that of the backward GRU (blue rectangle) is by $\bar{y}_b(t)$. After looking through all the words in the question, the hidden layer output of forward GRU network at the last time index $\bar{y}_f(T)$, and that of backward GRU network at the first time index $\bar{y}_b(1)$, are concantenated to form the question vector representation $\bar{V}_Q$, or $\bar{V}_Q=[\bar{y}_f(T)||\bar{y}_b(1)]$.

The symbol $[ \cdot || \cdot ]$ denotes concatenation of two vectors.

Story Attention Module

Fig.3B shows the attention mechanism which takes the question vector $\bar{V}_Q$ obtained in Fig.2A and the story transcriptions as the input to encode the whole story into a story vector representations $\bar{V}_S$.

The story transcription is a long word sequence with many sentences, only two sentences are shown, and each sentence is with 4 words for simplicity.

There is a bidirectional GRU in Fig.3(B) encoding the whole story into a story vector representation $\bar{V}_S$.

The word vector representation of the $t$-th word $\bar{S}_t$ is constructed by a concatenating the hidden layer outputs of forward and backward GRU networks, which is $\bar{S}_t=[\bar{y}_f(t) \Vert \bar{y}_b(t)]$.

Then the attention value $\alpha_t$ for each time index $t$ is the cosine similarity between the question vector $\bar{V}_Q$ and the word vector representation $\bar{S}_t$ of each word, $\alpha_t = \bar{S}_t \odot \bar{V}_Q$.

With attention values $\alpha_t$, there can be two different attention mechanisms, word-level and sentence-level, to encode the whole story into the story vector representations $\bar{V}_s$.

The symbol $\odot$ denotes cosine similarity between two vectors.

Word-level Attention

All the attention values $\alpha$ are normalized into $\alpha_t'$ such that they sum to one over the whole story. Then all the word vector $\bar{S}_t$ from the bidirectional GRU network for every word in the story are weighted with this normalized attention value $\alpha_t'$ and sum to give the story vector, i.e., $\bar{V}_S=\displaystyle \sum_{t} \alpha_t' \bar{S}_t$.

In other words, $\alpha_t'=\displaystyle \frac{\alpha_t}{\sum_t \alpha_t}$

Sentence-Level Attention

Sentence-level attention means the model collects the information only att the end of each sentence. Therefore, the normalization is only performed over those words tat the end of the sentences to obtain $\alpha_t"$.

The story vector representation is then $\bar{V}_S= \displaystyle \sum_{t=\textrm{Eos}} \alpha_t'' \times \bar{S}_t$, where only those words at the end of sentences (Eos) contribute to the weighted sum. So $\bar{V}_S = \alpha_4'' \times \bar{S}_4 + \alpha_t'' \times \bar{S}_8$ in the example of fig.2.

In other words,

$\alpha_t''=\displaystyle \frac{\alpha_t}{\sum_{t=\textrm{eos}} \alpha_t}$

Hopping

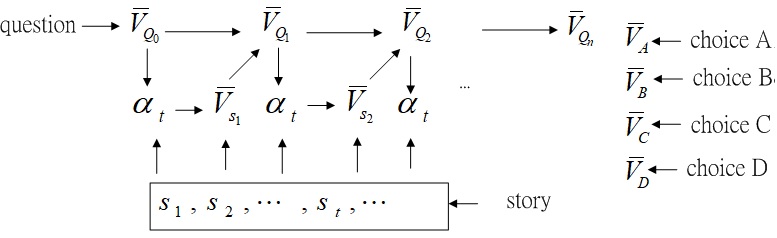
Fig.4 Overall data flow for AMRNN model.

Fig.4 shows the overall data flow for AMRNN model.

The overall picture of the proposed model is shown in fig.2, in which fig.3 (A) and (B) of the complete proposed model. In the left of fig.2, the input question is first converted into a question vector $\bar{V}_Q$ by module in Fig.3(A). This $\bar{V}_Q$ is used to compute the attention values $\alpha_t$ to obtain the story vector $\bar{V}_{S_1}$ by the module in Fig.3(B). Then $\bar{V}_{Q_0}$ and $\bar{V}_{S_1}$ are summed to form a new question vector $\bar{V}_{Q_1}$.

This process is called the first hop (hop1) in fig.2.

The output of the first hop $\bar{V}_{Q_1}$ can be used to compute the new attention to obtain a new story vector $V_{S_1}$.

This can be considered as the machine going over the story again to re-focus the story with a new question vector.

Again, $\bar{V}_Q$ and $\bar{V}_{S_1}$ are summed to form $\bar{V}_{Q_2}$ (hop2).

After $n$ hops, the output of the last hop $\bar{V}_{Q_n}$ is used for the answer selection in Answer Selection.

Answer Selection

As in the upper part of fig.1, the same way previously used to encode the question into $\bar{V}_Q$ in fig.2(A) is used here to encode four choice into choice vector representation $\bar{V}_A$, $\bar{V}_B,$ $\bar{V}_C$, $\bar{V}_D$.

Then the coin similarity between the output of the last hop $\bar{V}_{Q_n}$, and the choice vectors are computed, and the choice with highest similarity is chosen.

The symbol $[ \cdot || \cdot ]$ denotes concatenation of two vectors.

The symbol $\odot$ denotes cosine similarity between two vectors.

[0]

B. H. Tseng, S. S. Shen, H. Y. Lee, L. S. Lee, ``Towards machine comprehension of spoken content: Initial TOEFL listening comprehension test by machine," Towards machine comprehension of spoken content: Initial TOEFL listening comprehension test by machine, 2016.

[1] J. Chung, C. Gulcehre, K. Cho, and Y. Bengio, “Empirical evaluation

of gated recurrent neural networks on sequence modeling,”

arXiv preprint arXiv:1412.3555, 2014.

[2] K. Cho, B. van Merrienboer, D. Bahdanau, and Y. Bengio, “On ¨

the properties of neural machine translation: Encoder-decoder approaches,”

arXiv preprint arXiv:1409.1259, 2014.

[3] D. Bahdanau, K. Cho, and Y. Bengio, “Neural machine translation

by jointly learning to align and translate,” arXiv preprint

arXiv:1409.0473, 2014.