Cosine Similarity

MM 0530/2018

Introduction

Cosine similarity is a measure of similarity between two non-zero vectors of an inner product space that measures cosine of the angle between them [0-a].

The cosine of $0^\circ$ is 1, $\cos 0^\circ=1$, and

$\cos \theta <1$ if $0< \theta \leq 90^\circ$.

Cosine similarity is thus a judgement of orientation and not magnitude.

Two vectors with the same orientation have a cosine similarity of 1, two vectors at $90^\circ$ have a similarity of 0, and two vector diametrically opposed have a similarity of $-1$, independent of their magnitude.

Definition

The cosine of two non-zero vectors can be expressed as

$\bar{a} \cdot \bar{b} = \Vert \bar{a} \Vert \Vert \bar{b} \Vert \cos \theta$

Given two vectors of attributes, $\bar{a}$ and $\bar{b}$, the cosine similarity, $\cos \theta$ is represented using a dot product and magnitude as

$\textrm{similarity} = \cos \theta = \frac{\bar{a} \bar{b}}{\Vert \bar{a} \Vert \Vert \bar{b} \Vert}$

Cosine Similarity will generates a metric that says how related are two documents by looking at the angle instead of magnitude [0-b].

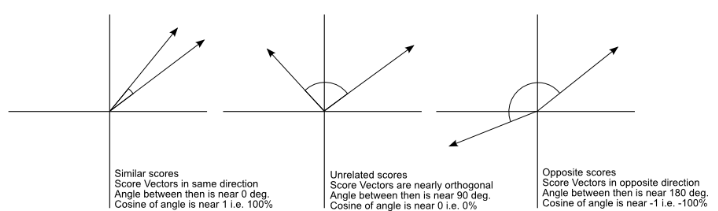Fig.1 The cosine similarity values for different documents, 1 (same direction), 0 (90 degree), -1 (opposite direction).

Fig.1 shows the cosine similarity, Cosine similarity is a judgement of orientation and not magnitude.

Practice Cosine Similairty Using Scikit-learn (sklearn)

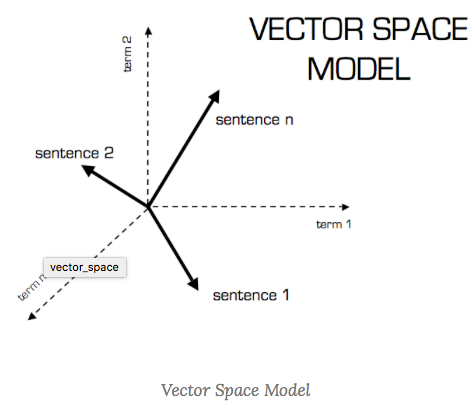Fig.2 Vector spce model

Fig. 2 shows the vector space model of documents modeled as vectors (with TF-IDF counts) .

Python 2.7.5 and Scikit-learn 0.14.1 are used.

The set of example documents should be defined

documents = (
"The sky is blue",
"The sun is bright",
"The sun in the sky is bright",
"We can see the shining sun, the bright sun"
)

Then, instantiate the Sklearn TF-IDF Vectorizer and transform the documents into the TF-IDF matrix

from sklearn.feature_extraction.text import TfidfVectorizer
tfidf_vectorizer = TfidfVectorizer()
tfidf_matrix = tfidf_vectorizer.fit_transform(documents)
print tfidf_matrix.shape
(4, 11)

TF-IDF matrix (tfidf_matrix) are created for each document (the number of rows of the matrix) with 11 tf-idf terms (the number of columns from the matrix). The cosine similarity between the first document (''The sky is blue'') with each of the other document can be calculated.

from sklearn.metrics.pairwise import cosine_similarity
cosine_similarity(tfidf_matrix[0:1], tfidf_matrix)
array([[ 1.        ,  0.36651513,  0.52305744,  0.13448867]])

The tfidf_matrix[0:1] is the Scipy operation to get the first row of the sparse matrix and the resulting array is the cosine similarity between the first document with all documents in the set.

Note that the first value of the array is 1, because it is the cosine similarity between the first document with itself. Also note that due to the presence of similar word on the third document (''The sun in the sky is bright''), it achieved a better score.

The angle can be obtained by using inverse of the cosine

$\theta=\textrm{arc cos} \frac{\bar{a} \cdot \bar{b}}{\Vert \bar{a} \Vert \Vert \bar{b} \Vert}$

The angle between the first and third documents are checked.

import math
# This was already calculated on the previous step, so we just use the value
cos_sim = 0.52305744
angle_in_radians = math.acos(cos_sim)
print math.degrees(angle_in_radians)
58.462437107432784

[0-a]

https://en.wikipedia.org/wiki/Cosine_similarity

[0-b]

http://blog.christianperone.com/2013/09/machine-learning-cosine-similarity-for-vector-space-models-part-iii/